Bottom-Up and Top-Down Reasoning with Hierarchical Rectified Gaussians
| Peiyun Hu | Deva Ramanan |
Abstract
Convolutional neural nets (CNNs) have demonstrated remarkable performance in recent history. Such approaches tend to work in a unidirectional bottom-up feed-forward fashion. However, practical experience and biological evidence tells us that feedback plays a crucial role, particularly for detailed spatial understanding tasks. This work explores bidirectional architectures that also reason with top-down feedback: neural units are influenced by both lower and higher-level units.
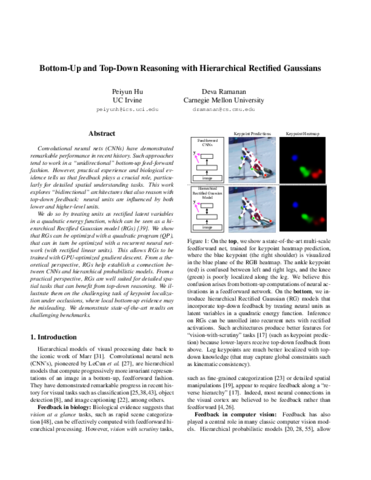
We do so by treating units as rectified latent variables in a quadratic energy function, which can be seen as a hierarchical Rectified Gaussian model (RGs). We show that RGs can be optimized with a quadratic program (QP), that can in turn be optimized with a recurrent neural network (with rectified linear units). This allows RGs to be trained with GPU-optimized gradient descent. From a theoretical perspective, RGs help establish a connection between CNNs and hierarchical probabilistic models. From a practical perspective, RGs are well suited for detailed spatial tasks that can benefit from top-down reasoning. We illustrate them on the challenging task of keypoint localization under occlusions, where local bottom-up evidence may be misleading. We demonstrate state-of-the-art results on challenging benchmarks.